Sudoku Strategies: X-Wings

Mastering the Sudoku X-Wing Technique

The X-wing is an advanced Sudoku solving strategy used to eliminate candidates for a single digit, often found in medium to hard puzzles. It is named for the X-like pattern (or a rectangle) formed by four cells in the grid, all containing the same candidate number.

How the X-Wing Works

The logic of the X-wing is based on the fundamental rule that each digit can only appear once in any given row or column. When a specific digit is a candidate in only two cells within two parallel rows (or columns), those cells must be the eventual location for that digit in those rows, which allows for eliminations in the shared columns (or rows).

Step-by-Step Guide to Using the X-Wing

Follow these steps to identify and apply the X-wing technique in a Sudoku puzzle:

1. Identify a single candidate number (e.g., the number 7) that appears exactly twice in a specific row (or column).
2. Locate a second, parallel row (or column) where the *same* candidate number also appears exactly twice.
3. Verify alignment. The potential cells for the candidate in the first row must be in the same two columns as the potential cells in the second row, forming the corners of a rectangle.
4. Apply the logic. In a valid X-wing, the candidate must exist in one of two diagonal pairs (either top-left/bottom-right or top-right/bottom-left). Regardless of which pair is the correct solution, one instance of the candidate will always be present in each of the two shared rows.
5. Eliminate other candidates. You can now safely eliminate that specific candidate number from any other cell within those two shared columns (or rows, if you started with a vertical X-wing).

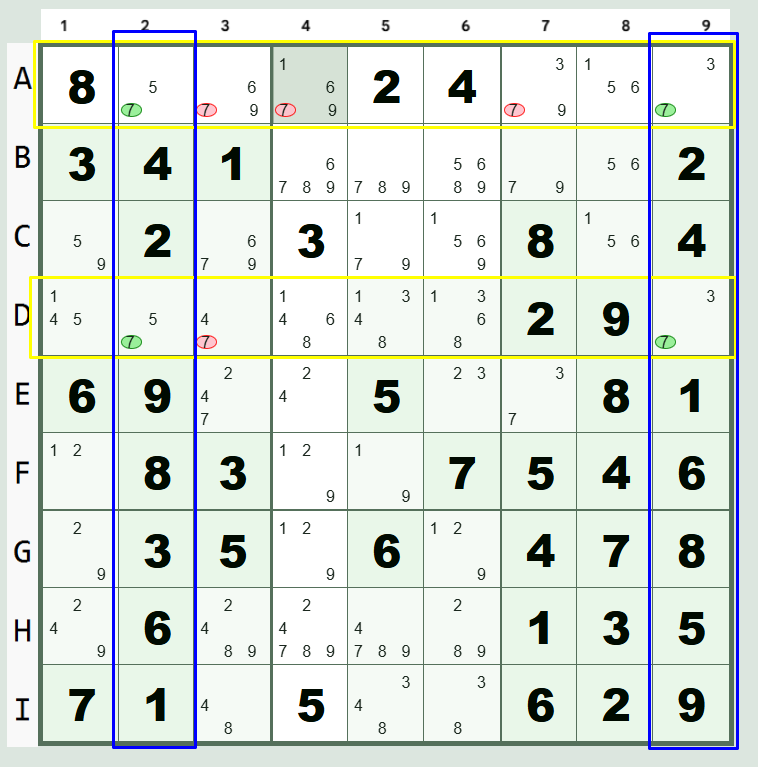
Example Illustration (Conceptual)

Imagine we find an X-wing for the candidate 7 in Column 2 and Column 9, specifically in Row "A" and Row "D".

In this conceptual example:

The cells at ("A2" and "D2" / "A9" and "D9") are the only possible spots for the number 7 within their respective columns.

Since a `7` must appear in two of the four intersection cells ("A2" and "D9" OR "D2" and "A9") we know that Rows "A" and "D" will each contain a `7` within the X-wing structure.

Therefore, any other candidate `7` in Row "A" or Row "D" can be removed from other rows. See illustration for eliminations highlighted in red.

The X-wing technique is a powerful way to make significant progress in challenging Sudoku puzzles and works best when you have fully marked your candidates in the grid.