Sudoku Strategies: Simple Coloring 1

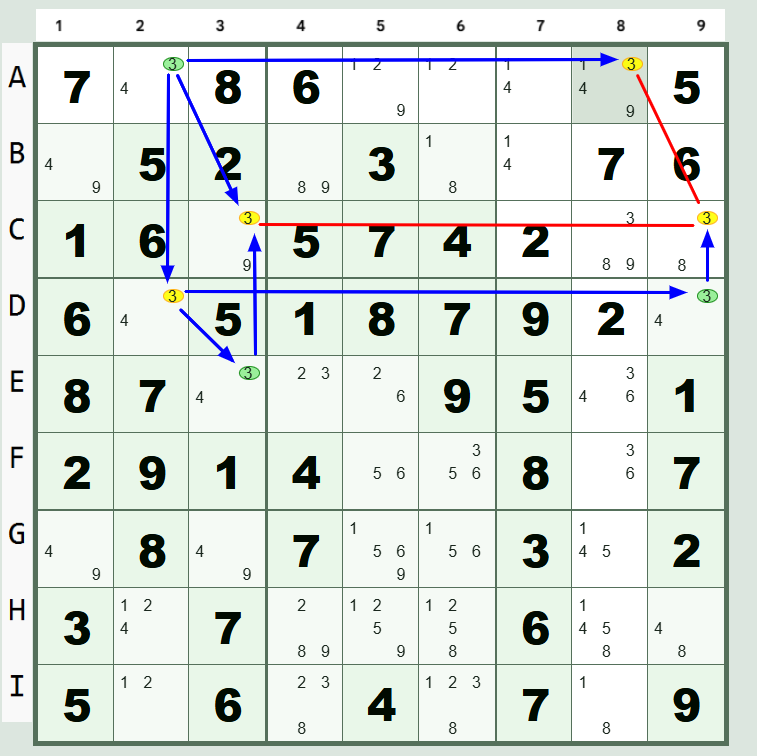
The Sudoku Simple Coloring (Rule 1) Technique

Simple Coloring is a powerful, single-digit advanced solving strategy that helps eliminate candidates by identifying logical relationships (chains) between potential cell values using only two colors. It is an efficient way to trace conjugate pairs - instances where a candidate appears exactly twice within a single region (row, column, or 3x3 box).

How Simple Coloring Works (Step-by-Step)

The core idea is that for any given candidate and its conjugate pairs, either all cells of one color are true, or all cells of the other color are true. Only one "state" can be the solution.

1. Pick a Candidate: Choose a single digit (e.g., the candidate "3") that appears in several conjugate pairs across the grid.
2. Start Coloring a Chain: Find a cell with that candidate that is part of a conjugate pair. Assign it one color (e.g., **Color A**, represented as green).
3. Follow the Links: The other cell in that conjugate pair must have the opposite color (**Color B**, represented as yellow) because one of them *must* be the solution for that region. Continue this alternating color process across the entire chain of linked conjugate pairs, extending as far as possible.
4. Scan for Contradictions (Deductions): Once the coloring is complete, look for scenarios that break the fundamental rules of Sudoku. There are two main types of deductions:
   • Rule 1: Color Contradiction (Same Color in a Unit): If two cells marked with the *same* color (green and green, or yellow and yellow) can see each other (share a row, column, or box), this is impossible. That color state is invalid, meaning all candidates of that color must be false and can be eliminated. All candidates of the *other* color must be the correct solution.
   • Rule 2 (not shown in illustration): Color Trap (Uncolored Cell Sees Both Colors): If an uncolored cell containing the target candidate can see two *differently* colored cells (one green and one yellow) within its region, the candidate in the uncolored cell must be false. Since one of the colored candidates must be the correct solution, the uncolored cell cannot also be the solution.
5. Eliminate and Solve: Eliminate the identified false candidates from their cells. This often creates new singles or other patterns that help solve the puzzle further.