Sudoku Strategies: Pointing Pairs
Pointing Pairs (or Pointing Triples)
An intermediate Sudoku technique used to eliminate candidate numbers from a row or column based on their distribution within a 3x3 box. It is part of a larger family of strategies known as Intersection Removal or Locked Candidates.
The Core Logic
The technique is based on a simple "either/or" requirement:
- Every 3x3 box must contain the numbers 1–9 exactly once.
- If a specific candidate digit (e.g., the number 4) appears only in one row or column within a 3x3 box, it must occupy one of those positions to satisfy the box's requirement.
- Because the digit is guaranteed to be in that specific row or column for that box, it cannot possibly appear in any other cell in that same row or column outside that box.
How to Identify and Solve
- Select a 3x3 Box: Examine the candidate notes for a specific digit within one box.
- Check Alignment: Look for a digit that only appears in two or three cells within that box, and confirm they all lie on the same straight line (row or column).
- Confirm Exclusion: Ensure the digit does not appear anywhere else in that same 3x3 box outside of that row or column.
- Execute Elimination: Follow that line into neighboring boxes. Remove that digit from the candidate notes of all other cells in that entire row or column.
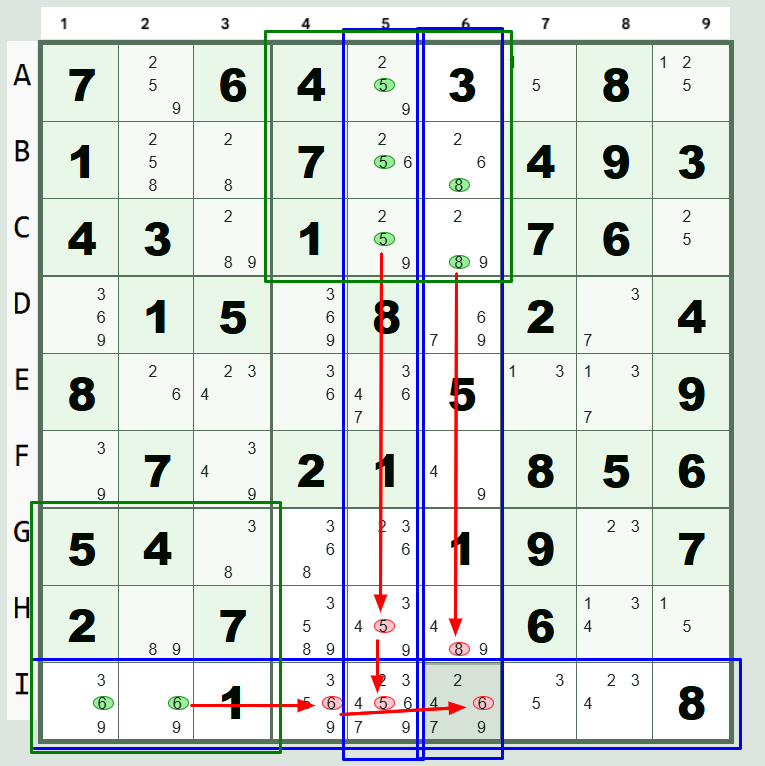
Examples (the following references image above)
- In box 2 there are two different set of pointing candidates. In box 2 / column 5 we can see there are 3 "5" candidates and there are no other "5" candidates in the box. So we know that any other 5 candidate in that column cannot be the solution and they can be eliminated.
- Similarly, in box 2 / column 6 there are 2 "8" candidates, but there are no other "8" candidates in box 2. Therefore the other "8" candidates in row 6 can be eliminated.
- Lastly, in box 7 / row I there are 2 "6" candidates, but there are no other "6" candidates in box 7. Therefore the other "6" candidates in row I can be eliminated.
Key Distinction: Pointing vs. Claiming
While often confused, they are "flip opposites" of each other:
Pointing
A box restricts a row/column. You find candidates locked in a box's line and eliminate them from the rest of that line outside the box.
Claiming
A row/column restricts a box. If all candidates for a digit in a row exist only inside one 3x3 box, you eliminate that digit from the rest of that box outside that row.

