Sudoku Strategies: Naked Triples
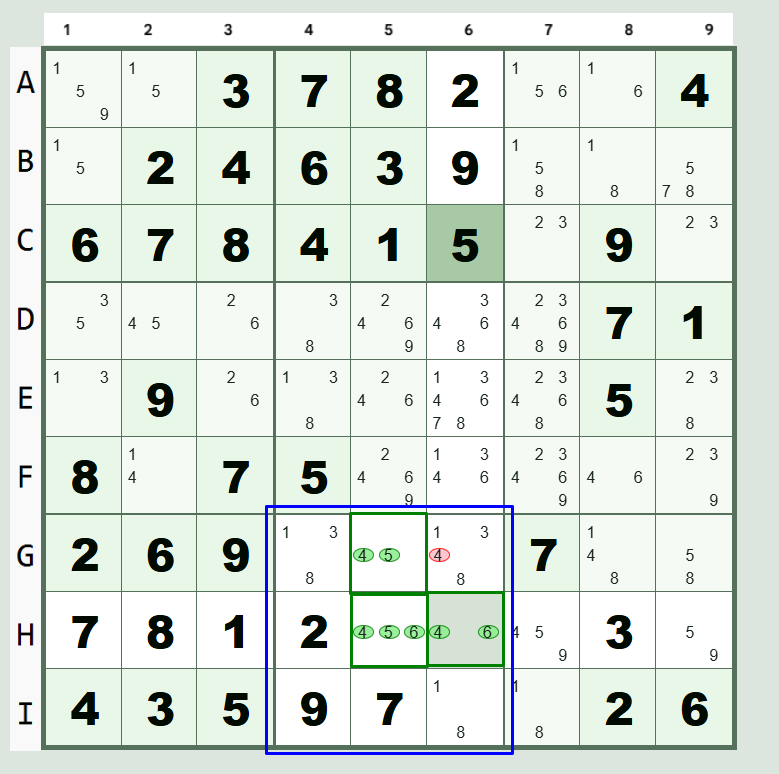
Naked Triples in Sudoku
A naked triple in Sudoku involves understanding that it is an advanced solving technique used when standard methods (like single candidates) no longer work.
Definition of a Naked Triple
A naked triple occurs when three different cells within the same house (a row, a column, or a 3x3 box) contain the exact same three potential candidates among them, and these three candidates appear nowhere else within that specific house.
In the illustration the key numbers involved form the "triple" (e.g., 4, 5, and 6). The cells containing these numbers are "naked" because they are stripped down to only those specific possibilities. The rule: as long as three cells in the given house (row, column, or 3x3 box) contain only the same 3 digits between all three cells, you can eliminate those candidates in the rest of that house.
The configuration can be 3/3/3 (e.g., 4,5,6/4,5,6/4,5,6), 2/3/2 (e.g., 4,5/4,5,6/4,6), 2/3/3 (e.g., 4,5/4,5,6/4,5,6), or 2/2/2 (e.g., 4,5/5,6/4,6). Not every candidate in the naked triple pattern has to appear in all three cells.
How to Identify a Naked Triple
To find a naked triple, you look for a group of three cells within a single house where the candidate lists, when combined, contain only three unique digits.
In all valid naked triples, the critical insight is that those three specific digits must occupy those three specific cells in some order. No other digit can go into those cells.
How to Use a Naked Triple (The Elimination Step)
Once a naked triple is identified, the solving strategy is straightforward:
- Identify the three digits involved in the triple (e.g., 4, 5, 6).
- Locate all other cells in that same row, column, or 3x3 box.
- Eliminate the triple's digits (4, 5, and 6) from the candidate lists of all those other cells within that house.
This elimination process significantly reduces the complexity of the puzzle. By removing impossible candidates from the surrounding cells, it often reveals singles (cells with only one remaining candidate) or other advanced patterns that allow you to continue solving the Sudoku puzzle.

