Sudoku Strategies: Hidden Triples

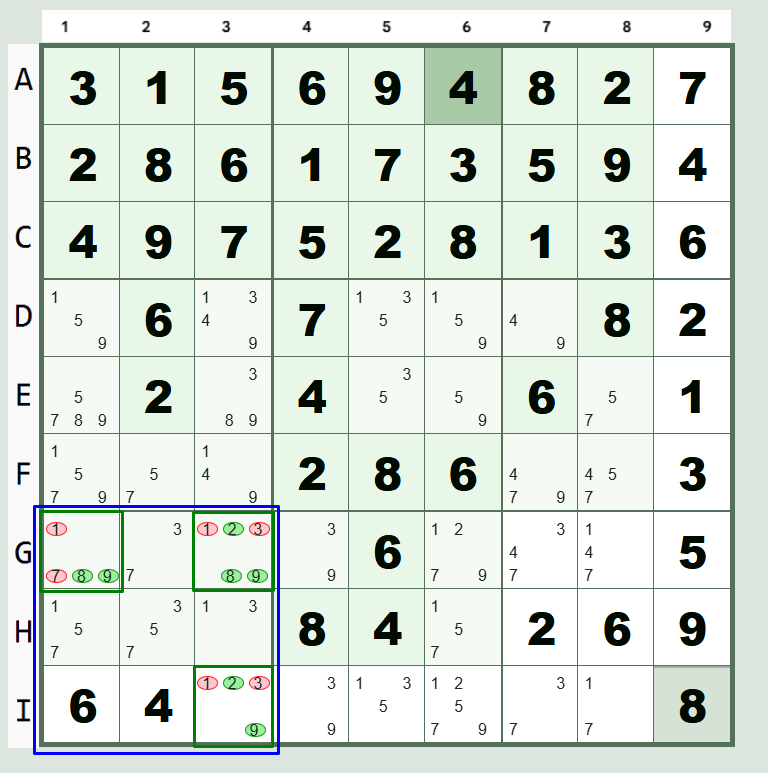
Understanding Hidden Triples in Sudoku

A Hidden Triple in Sudoku occurs when a specific set of three candidate numbers can only appear in three cells within a single unit (a row, column, or 3x3 block). These three cells contain other candidate numbers, which "hide" the triple, making it less obvious than a naked triple.

The key logic is that because these three numbers have no other possible locations within that unit, they must reside in those specific three cells. Therefore, any other candidate numbers in those three cells can be safely eliminated.

How to Identify and Use a Hidden Triple

Identifying a hidden triple requires careful scanning of the potential candidates within a unit. The process is as follows:

• Note all candidates: Fully annotate all potential candidate numbers for each cell in the Sudoku grid, especially in more difficult puzzles.
• Scan by unit: Focus on a single row, column, or 3x3 block that has several empty cells.
• Look for unique candidate locations: Search for three specific numbers (e.g., 2, 8, and 9) that only appear as candidates in the same three cells within that unit.
• Verify the criteria:
  • The three cells may contain more candidates than just the target three numbers (e.g., one cell "G3" might have 1, 2, 3, 8, 9 as candidates).
  • The crucial condition is that the numbers of the hidden triple (2, 8, and 9 in this example) do not appear as candidates in any of the other cells in that same unit.
• Eliminate extra candidates: Once a hidden triple is confirmed, you can eliminate all other candidates from those three specific cells. For the cell "G3" with {1, 2, 3, 8, 9}, you would remove the '1' and '3' candidates, leaving only {2, 8, 9}. This elimination often leads to a cascade of other deductions, helping to solve the puzzle faster.

By scanning the highlighted box, you notice the numbers 2, 8, and 9 only appear as candidates in cells "G1", "G3", and "I3". In all other cells in the house/unit, the numbers 2, 8, or 9 are not present.

Therefore, {2, 8, 9} form a hidden triple. The '1' and '7' and '3' candidates in cells "G1", "G3", and "I3" can be removed.