Sudoku Strategies: Hidden Quads
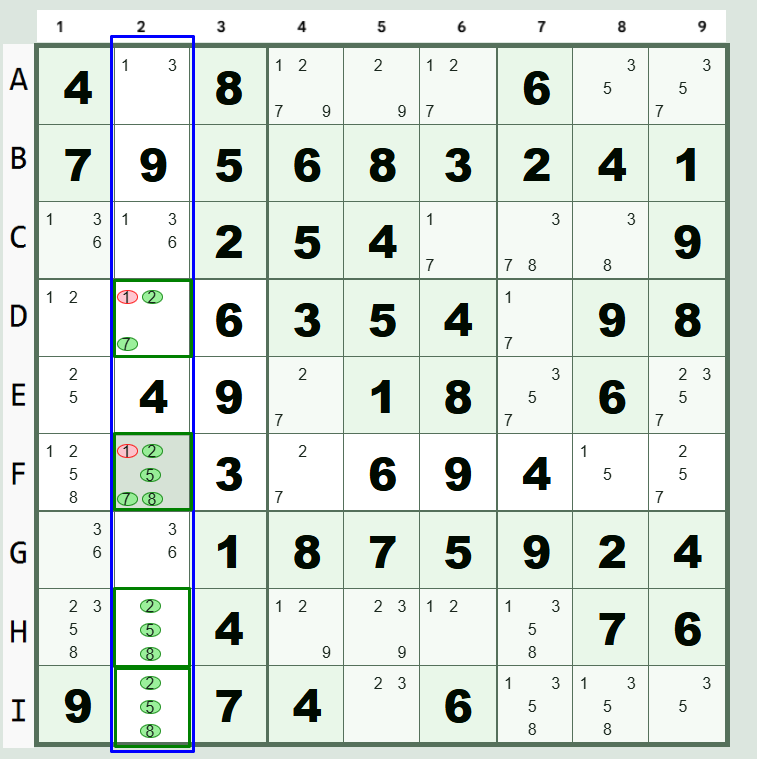
Understanding Hidden Quads in Sudoku
A Hidden Quad (or Hidden Quadruple) is an advanced Sudoku technique used when four candidate numbers appear only within four specific cells in a single unit (a row, column, or 3x3 block), even if those cells contain other candidates. Once identified, all other candidates in those four cells can be eliminated.
The Hidden Quad is a powerful, yet tricky to spot, advanced Sudoku strategy. It helps reduce possibilities when other basic techniques are no longer effective.
What is a Hidden Quad?
A Hidden Quad occurs when:
- Four specific candidate numbers (e.g., 2, 5, 7, 8) appear in only four cells within a single house (row, column, or block).
- These four cells might contain other "extra" candidates, which is what makes the quad "hidden" from plain view.
- The four candidates, as a set, do not appear in any other cell within that same house.
The logical deduction is that since those four numbers must be placed somewhere in the unit, they are "locked in" to those four specific cells. Therefore, any other candidate numbers in those four cells can be safely removed.
How to Identify and Use a Hidden Quad
Follow these steps to find and apply the Hidden Quad strategy:
- Mark All Candidates: Ensure all possible candidates (pencil marks) are filled in for the relevant unit. This is essential for spotting hidden subsets.
- Systematic Scanning: Scrutinize each row, column, and 3x3 block for four specific numbers that seem to appear infrequently. Check for Exclusivity: Verify that these four candidates only appear in exactly four cells within that unit. The set of numbers across those four cells must collectively represent all four candidates. Eliminate Extra Candidates: Once confirmed, remove all other candidates that are not part of the hidden quad from those four specific cells. `
- D2: {1, 2, 7}
- F2: {1, 2, 5, 7, 8}
- H2: {2, 5, 8}
- I2: {2, 5, 8}
Example in a Column
Consider a row with four cells (let's call them C1, C2, C3, C4) containing the following candidates:
By checking the entire column, you observe that the candidates 2, 5, 7, and 8 only appear in these four cells and nowhere else in that row. This is a Hidden Quad.
The result is that you can eliminate all other candidates. In this case we can make two eliminations 1) The quad eliminates "1" in cell "D2" and another "1" from cell "F2".
Why it Works
The fundamental logic is based on necessity. There are four unique positions in the unit that must be filled by four unique numbers (1 through 9). If four specific numbers can only go into a specific set of four cells, then they must go into those cells. Placing any of those four numbers in any other cell within that unit would leave one of the four designated cells without a possible candidate, which is impossible in a valid Sudoku puzzle.

