Sudoku Strategies: Box-Line Reduction

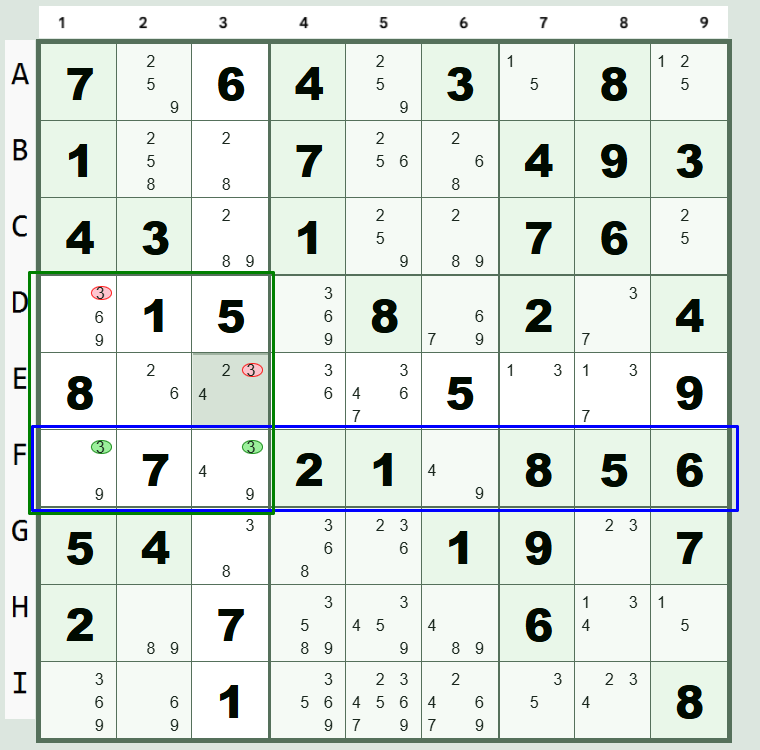
Box-Line Reduction (Claiming)

Box-Line Reduction, also known as Claiming, is an elimination strategy based on the intersection of a line (row or column) and a 3x3 box. It is the logical inverse of the Pointing Pairs technique.

Core Logic

The strategy is used when all possible cells for a specific candidate within a line (row or column) are located inside a single 3x3 box. Since that number must appear somewhere in that row/column, it is "claimed" by the intersection area. This means the number cannot appear anywhere else in that same 3x3 box.

Step-by-Step Execution

• Select a Candidate: Pick a candidate (e.g., ""3") and scan its possible positions across the grid.
• Find a Restricted Line: Look for a row or column where the candidate "3" only appears in 2 or 3 cells, and all those cells belong to the same 3x3 box.
• Perform Elimination: Because the 3 must be in one of those 2 or 3 cells to satisfy the row/column requirement, it cannot be placed in any other cell within that 3x3 box.
• Remove Candidates: Erase all other "5" pencil marks from the cells in that box that are not part of the original row/column.

Key Comparison: Pointing vs. Claiming

These two techniques are often grouped together as Intersection Removal.

• Pointing (Type 1): You look at a Box first. If a candidate in a box is restricted to one line, you eliminate it from the rest of that Line.
• Claiming / Box-Line Reduction (Type 2): You look at a Line first. If a candidate in a line is restricted to one box, you eliminate it from the rest of that Box.

Example Scenario

Row "F". You notice that for the candidate "3", there are no other candidate "3"s in row "F". Therefore the "3" candidate must reside in one of those two cells ("F1" OR "F3"). Knowing this, we can eliminate all other candidate "3"s in box 4 (eliminations in cells "D1" AND "D3").